Heb je hier wat aan gehad? Abonneer dan op mijn YouTube kanaal: ![]()
Doneer meneer Wietsma een kopje koffie: ![]()
Klik hier voor een samenvatting van de video
Wanneer een atoom vervalt verandert het en is het niet meer hetzelfde atoom. Je kunt je dus voorstellen dat het vervallen op een gegeven moment stopt omdat de atomen weg zijn. Als je aan het begin 100 g van een radioactieve stof hebt dan zal dit veranderen naar een andere stof. Stel dat je na 4 dagen nog maar 50 g van de beginstof meet, kun je zeggen dat de halveringstijd of halfwaardetijd van de stof 4 dagen was. Wacht je nogmaals 4 dagen dan is wee de helft weg en heb je nog maar 25 g van de beginstof. Dit gaat zo door totdat ook het laatste atoom vervallen is.
De halveringstijd en halfwaardetijd kunnen erg verschillen tussen stoffen. Het kan van microsecondes tot aan miljarden jaren zijn. Vaak moet je de halfwaardetijd/halveringstijd uit een grafiek halen
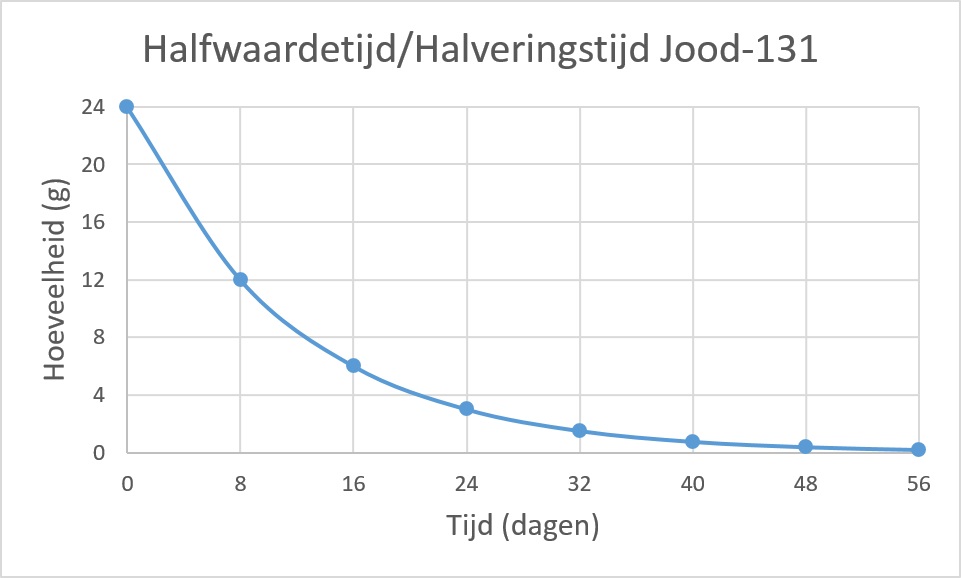
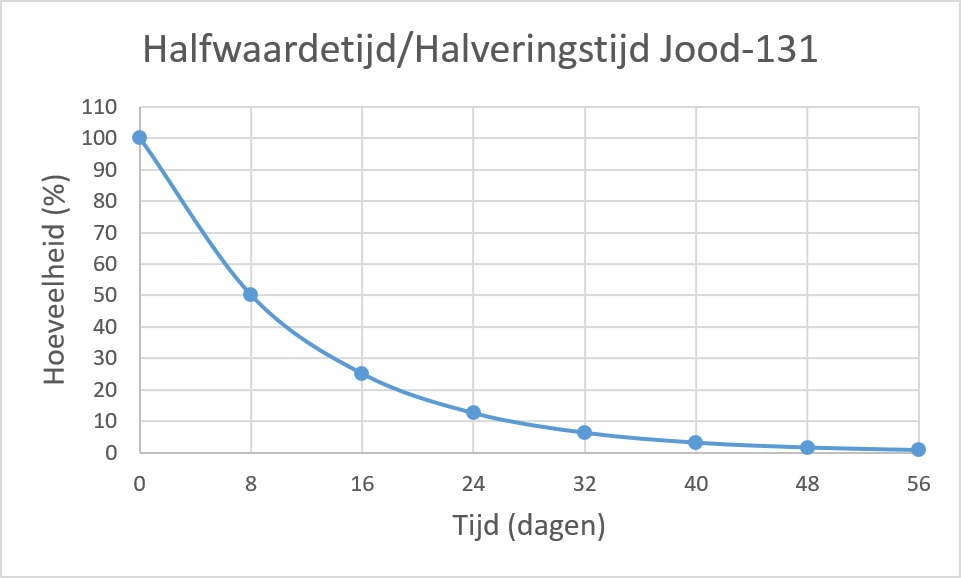
Hierboven zie je twee grafieken van Jood-131. De ene geeft de hoeveelheid aan in procenten de andere in grammen. Beide kun je gebruiken om de halveringstijd/halfwaardetijd te bepalen. In dit geval dus 8 dagen.
Quiz-summary
0 of 7 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
Maak de quiz om te zien of je het snapt
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Resultaten
0 van de 7 vragen goed
Time has elapsed
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Beantwoord
-
Vraag 1 van 7
1. Question
Je hebt twee verschillende stoffen (zelfde hoeveelheid), A met een halveringstijd/halfwaardetijd van 3 minuten en B met een halveringstijd/halfwaardetijd van 5400 jaar. Welke stof blijft langer intact?
Correct
Incorrect
-
Vraag 2 van 7
2. Question
Je hebt drie verschillende stoffen, A met een halveringstijd/halfwaardetijd van 3 minuten die vervalt met een bèta deeltje, B met een halveringstijd/halfwaardetijd van 5400 jaar die vervalt met een bèta deeltje en stof C met een halveringstijd/halfwaardetijd van 5 minuten die vervalt met twee bèta deeltjes. Van welke stof komt per seconde de meeste ioniserende straling?
Correct
Incorrect
-
Vraag 3 van 7
3. Question
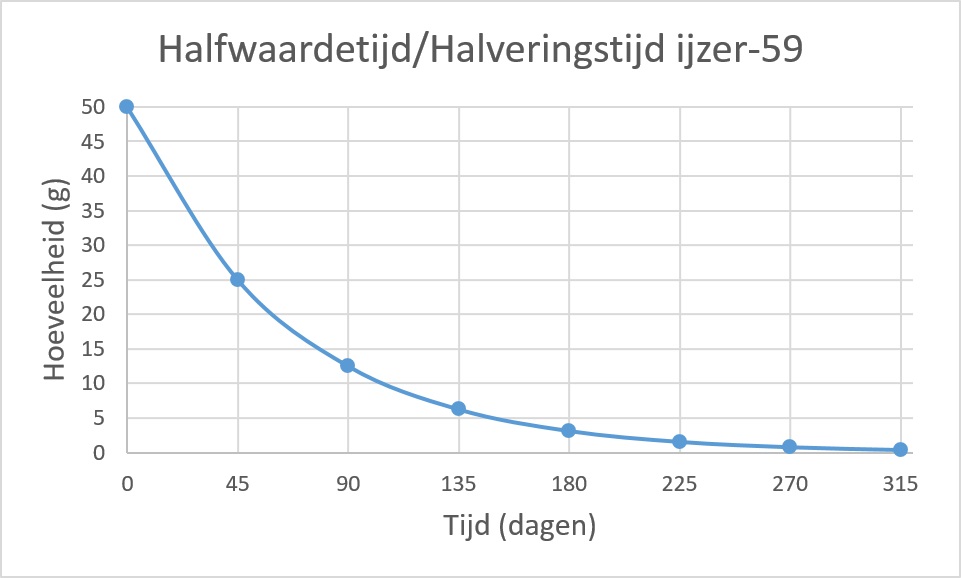
Hoe groot is de halveringstijd/halfwaardetijd van ijzer?- (45) dagen
Correct
Incorrect
-
Vraag 4 van 7
4. Question
Stel je hebt 432 gram ijzer-59 met een halveringstijd/halfwaardetijd van 45 dagen. Hoeveel heb je dan nog na 180 dagen?
- (27) g
Correct
Incorrect
-
Vraag 5 van 7
5. Question
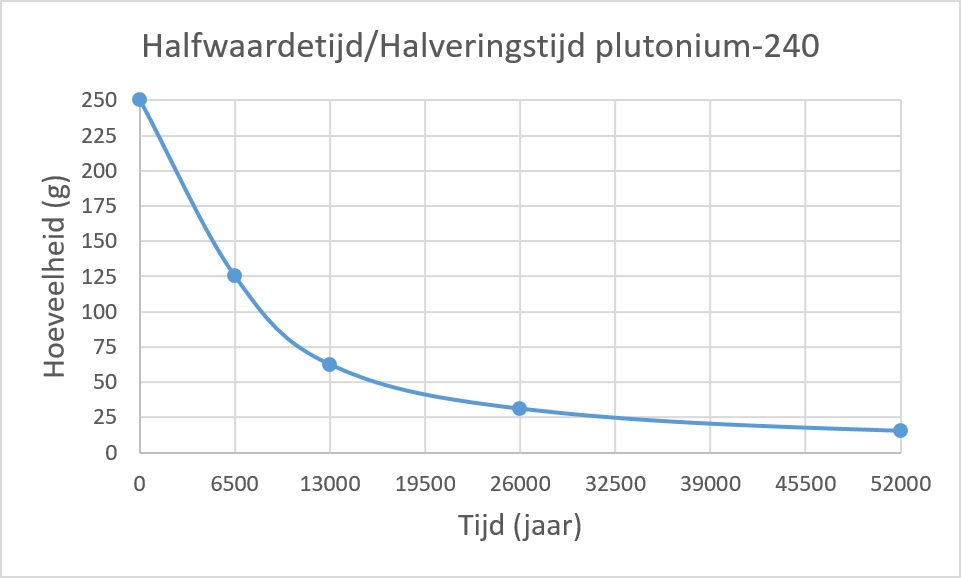
Hoe groot is de halveringstijd/halfwaardetijd van plutonium-240?- (6500) jaar
Correct
Incorrect
-
Vraag 6 van 7
6. Question
Stel je hebt 500 g plutonium-240 met een halveringstijd/halfwaardetijd van 6500 jaar. Hoe lang duurt het dan voordat je nog maar 15,625 g hebt?
- (32500) jaar
Correct
Hoeveelheid (g) Tijd (jaar) 500 0 250 6500 125 13000 62,5 19500 31,25 26000 15,625 32500 Incorrect
Hoeveelheid (g) Tijd (jaar) 500 0 250 6500 125 13000 62,5 19500 31,25 26000 15,625 32500 -
Vraag 7 van 7
7. Question
Je hebt 40 g Ag-110. Na 125 seconden heb je nog maar 1,25 g. Wat is de halveringstijd/halfwaardetijd van Ag-110?
- (25) s
Correct
In totaal is de halveringstijd/halfwaardetijd 5 keer geweest om van 40 naar 1,25 te gaan (40/2/2/2/2/2 = 1,25 of 40/25 = 1,25.
Dus 125 / 5 = 25 s
Incorrect
In totaal is de halveringstijd/halfwaardetijd 5 keer geweest om van 40 naar 1,25 te gaan (40/2/2/2/2/2 = 1,25 of 40/25 = 1,25.
Dus 125 / 5 = 25 s


Laat een bericht achter
16 berichten op "Halveringstijd Halfwaardetijd"
leuke quiz helpt bij de toets
Kunt u er een flimpje zetten over de halveringsdikte en stralingsdosis, ik moet het voor volgende week al geleerd hebben
Alvast bedankt
Die staan op de planning, maar momenteel ben ik bezig met examen video’s dus helaas niet af voor volgende week.
Is goed
wat is een ioniserende straling?
Dat is straling dat stoffen kan veranderen (ioniseren). Bijvoorbeeld alfa, beta, gamma, röntgen en UV straling. Soms wordt deze straling ook radioactive straling genoemd, maar die term is helaas fout.
Vraag 1 kan je toch technisch gezien niet weten sinds je de hoeveelheid van de stoffen niet weet.
Helemaal gelijk! Aangepast
volgens mij klopt vraag 4 niet helemaal want ik kom steeds op 54 uit. Kunt u er even naar kijken
De halveringstijd is 45 dagen. Na 180 dagen is er: 180 / 45 = 4 keer gehalveerd.
Je had 432 gram, dus:
432 / 2 / 2 / 2 / 2 = 27 gram is over.
ik snap vraag 2 niet. Hoe moet je dit toepassen?
Je hebt 3 stoffen
A halfwaardetijd 3 minuten en er komt 1 beta deeltje vrij
B halfwaardetijd 5400 jaar en er komt 1 beta deeltje vrij
C halfwaardetijd 5 minuten en er komen 2 beta deeltjes vrij
Bij welke stof komt de meeste straling per seconde vrij? Dat is diegene met de kleinste halfwaardetijd en de meeste straling die vrij komt. Van C zou je kunnen zeggen dat die een halfwaardetijd van 2,5 minuut heeft als er maar 1 beta deeltje vrij komt (dit klopt niet, maar op die manier kun je het vergelijken). Dus C
Hallo, zou iemand mij kunnen helpen met onderstaande vraag?
De halfwaardetijd van jodium is 8 dagen en het ziekenhuis koopt 12,4 gram aan. Onderstel exponentiële groei (verval). Hoelang duurt het (in dagen) om 3,6 gram over te houden?
Voor de onderbouw:
Het makkelijkste is om een tabel te maken:
12,4 gram op dag 0
6,2 gram op dag 8
3,1 gram op dag 16
Dus ongeveer op dag 14
Voor de bovenbouw (https://meneerwietsma.nl/straling/halveringstijd-berekenen/):
Je kunt het berekenen met: m(t) = m0 * 0,5^(t/t1/2). Kijk in je boek of je deze formule moet kennen, zo niet, negeer dan wat hier onderstaat
m(t) = 3,6 gram
m(0) = 12,4 gram
t1/2 = 8 dagen
Invullen:
m(t) = m0 * 0,5^(t/t1/2)
3,6 = 12,4 * 0,5^(t/8)
Delen door 12,4
0,29 = 0,5^(t/8)
Macht wegwerken:
log(0,29)/log(0,5) = t/8
1,786 = t/8
maal 8
t = 1,786 * 8 = 14 dagen
ik snap vraag 6 niet, want waarom gaat de sprong van jaren van 13000 naar 19500 het is niet 2 x 13000, dus met wat vermenigvuldig je het?
Bij de halveringstijd is het altijd + de halveringstijd en niet x2.
Dus bij die vraag doe je steeds +6500